Le langage pour Processing

.

Mise à jour le 25/12/2019 :Processing est tout particulièrement adapté à la création graphique interactive , mais sa simplicité d’utilisation en fait aussi aussi un bon support pour l’apprentissage de la programmation pour les non-programmeurs.

Sommaire :

Présentation de Processing
Utilisation de l’ecran
- Comment définir la taille de l’écran ou l’espace de travail ?
- Comment utilisé la taille max de l’ecran avec la Fonction fullSceen() ?
Couleur du fond d’écran.
- Comment changer la couleur du fond de l’écran ou de l’espace de travail ?
Différentes formes pour dessiner .
- Le rectangle (a,b,c,d)
Tableau des différentes formes dans Processing
- Le point .
  - Exemple de positionnement d’un point sur l’écran.
  - Exemple de création d’une ligne avec un ensemble de points.
- La ligne [ line ]
- Le rectangle [ rect ]
- Le rectangle avec un angle variable dans chaque coin.
- Ellipse [ ellipse ]
- Le triangle [ triangle ]
- L’arc [ arc ]
- Le quadrilatère
- La courbe
- La courbe de Bézier
  - La création d’un regard avec l’utilisation de la fonction courbe de Bezier et la fonction ellipse ( Tutoriel ).
Ecrire un texte a l’écran
- 001 – Ecrire un texte a l’écran , choix de la couleur , de la taille et positionnement.
- 004 – La typographie comment importer une police de caractères ( Tutoriel )
- 010 – Comment déplacer un texte avec la commande translate sans effacement de l’ancienne position.
Manipulation des fichiers images
- Sommaire général .
- Présentation de la fonction image
- Comment importer une image dans Processing ( Tutoriel ).
Utilisation de la souris dans Processing.
- Variable système attachées à l’utilisation de la souris
- Un cercle qui suit les mouvements de votre souris .
- Déplacement de forme avec la fonction mouseY
La lecture du son.
Communication entre les cartes Arduino et Processing
- La communication série Lecture d’un compteur dans la carte Arduino sur Processing communication série.
Retour à la page principal.

Présentation de Processing

Ci-dessous en gras un extrais du manuel sur le site : Flossmanuals

Processing est un logiciel libre et gratuit. Il fonctionne sur les plates-formes Windows, Linux, Mac (et sur toute autre plate-forme pouvant faire fonctionner des logiciels conçus en Java). Il existe également des versions pour téléphones portables et des dérivés pour circuits électroniques.

Un programme Processing se dissocie en 3 partie comme sur le logiciel Arduino , une partie pour les inclusions de bibliothèque et des variables , une autre pour la configuration dans la partie void setup (), et enfin une partie similaire à void loop dans la partie void draw () .

La fonction setup ()
Est exécutée une fois au démarrage du programme. Il est utilisé pour définir les propriétés initiales de l’environnement telles que la taille de l’écran et pour charger des supports tels que les images et les polices au démarrage du programme. Il ne peut y avoir qu’une seule fonction setup () pour chaque programme et il ne devrait plus être appelé après son exécution initiale.
Si l’esquisse est une dimension différente de celle par défaut, la fonction size () ou fullScreen () doit être la première ligne de setup () .
Remarque: Les variables déclarées dans setup () ne sont pas accessibles dans d’autres fonctions, y compris draw () .

La fonction draw ()

Appelée directement après la fonction setup () , la fonction draw () exécute en continu les lignes de code contenues dans son bloc jusqu’à ce que le programme soit arrêté ou que noLoop () soit appelé. draw () est appelé automatiquement et ne doit jamais être appelé explicitement.
Le nombre de fois que draw () s’exécute en une seconde peut être contrôlé avec la fonction frameRate () .

Il est courant d’appeler background () au début de la boucle draw () pour effacer le contenu de la fenêtre, . Étant donné que les pixels dessinés dans la fenêtre sont cumulatifs, la suppression de background () peut entraîner des résultats inattendus.

La largeur et la hauteur minimales sont d’environ 100 pixels dans chaque direction. C’est la plus petite prise en charge sous Windows, macOS et Linux. Nous appliquons la taille minimale afin que les esquisses s’exécutent de manière identique sur des machines différentes.
Le paramètre de rendu sélectionne le moteur de rendu à utiliser. Par exemple, si vous voulez dessiner des formes 3D, utilisez P3D . Outre le rendu par défaut, les autres rendus sont:

P2D(Processing 2D): rendu graphique 2D utilisant un matériel graphique compatible OpenGL.
P3D (Processing 3D): moteur de rendu graphique 3D utilisant un matériel graphique compatible OpenGL.
FX2D (JavaFX 2D): Un moteur de rendu 2D qui utilise JavaFX, qui peut être plus rapide pour certaines applications, mais présente des problèmes de compatibilité.
PDF : Le moteur de rendu PDF dessine des graphiques 2D directement dans un fichier PDF Acrobat. Cela produit d’excellents résultats lorsque vous avez besoin de formes vectorielles pour une impression haute résolution. Vous devez d’abord utiliser Importer la bibliothèque → PDF pour pouvoir utiliser la bibliothèque. Plus d’informations peuvent être trouvées dans la référence de la bibliothèque PDF.
SVG: Le moteur de rendu SVG dessine des graphiques 2D directement dans un fichier SVG. C’est idéal pour importer dans d’autres programmes vectoriels ou pour une fabrication numérique. Vous devez d’abord utiliser Importer la bibliothèque → Export SVG pour pouvoir utiliser la bibliothèque

A partir de Processing 3.0, pour utiliser des variables en tant que paramètres de la fonction size () , placez la fonction size () dans la fonction settings () (au lieu de setup () ).

Retour au sommaire

Utilisation de l’écran

–

Comment définir la taille de l’écran ou l’espace de travail ?

La fonction size ()

Définit la dimension de la largeur et de la hauteur de la fenêtre d’affichage en unités de pixels. Dans un programme doté de la fonction setup () , la fonction size () doit être la première ligne de code dans setup () , et la fonction setup () doit apparaître dans l’onglet de code avec le même nom que votre dossier de croquis.

La fonction size () ne peut être utilisée qu’une seule fois dans une esquisse et ne peut pas être utilisée pour le redimensionnement.

À partir de la version 3.x.x, pour exécuter une esquisse aux dimensions complètes d’un écran, utilisez la fonction fullScreen () , plutôt que l’ancienne méthode consistant à utiliser size (displayWidth, displayHeight) .

La largeur et la hauteur maximales sont limitées par votre système d’exploitation et correspondent généralement à la largeur et à la hauteur de votre écran actuel. Sur certaines machines, il peut simplement s’agir du nombre de pixels de votre écran actuel, ce qui signifie qu’un écran de 800 x 600 peut prendre en charge la taille (1600, 300)., puisque c’est le même nombre de pixels. Cela varie énormément, vous devrez donc essayer différents modes et tailles de rendu jusqu’à obtenir ce que vous cherchez. Si vous avez besoin de quelque chose de plus grand, utilisez createGraphics pour créer une surface de dessin non visible.

//
// Comment définir la taille de l’écran  ou de l'espace de travail
// dans processing
//
// H-Mazelin le 12/06/2017 


// La fonction setup () est exécutée une fois, lorsque le programme démarre. 
// Il sert à définir les propriétés d'environnement initiales telles que la 
// taille de l'écran et à charger des supports tels que des images et des polices
// au démarrage du programme. 


void setup ()
{
  // definition de la taile de la fenetre 
  // syntaxe : size (Hauteur fenetre,largeur fenetre )
  size(600,400);
  // choix de la couleur du fond de la fenetre 
  // syntaxe : background (rouge,vert,bleu )
  // valeur du rouge de 0 à 255 iden pour les autre couleurs
  background(255,255,255);
  
}


//Le programme principal s’exécute par une boucle infinie appelée draw () 
void draw ()

{
  
 
  
}

// Comment définir la taille de l’écran ou de l'espace de travail

// dans processing

// H-Mazelin le 12/06/2017

// La fonction setup () est exécutée une fois, lorsque le programme démarre.

// Il sert à définir les propriétés d'environnement initiales telles que la

// taille de l'écran et à charger des supports tels que des images et des polices

// au démarrage du programme.

void setup ()

{

// definition de la taile de la fenetre

// syntaxe : size (Hauteur fenetre,largeur fenetre )

size(600,400);

// choix de la couleur du fond de la fenetre

// syntaxe : background (rouge,vert,bleu )

// valeur du rouge de 0 à 255 iden pour les autre couleurs

background(255,255,255);

}

//Le programme principal s’exécute par une boucle infinie appelée draw ()

void draw ()

{

}

Retour au sommaire

Fonction fullSceen()

Cette fonction est nouvelle pour Processing 3.0. Il ouvre une esquisse en utilisant toute la taille de l’écran de l’ordinateur. Cette fonction doit être la première ligne de setup () . Les fonctions size () et fullScreen () ne peuvent pas être utilisées dans le même programme, il suffit de choisir un.

Lorsque fullScreen () est utilisé sans paramètre, il dessine l’esquisse sur l’écran actuellement sélectionné dans la fenêtre Préférences. Lorsqu’il est utilisé avec un seul paramètre, ce numéro définit l’écran à afficher pour programmer (par exemple, 1, 2, 3 …). Lorsqu’il est utilisé avec deux paramètres, le premier définit le moteur de rendu à utiliser (par exemple, P2D) et le second définit l’écran. Le SPAN Ce paramètre peut être utilisé à la place d’un numéro d’écran pour dessiner l’esquisse sous la forme d’une fenêtre plein écran sur tous les écrans attachés, s’il en existe plusieurs.

Avant Processing 3.0, un programme en plein écran était défini avec size(displayWidth, displayHeight).

Retour au sommaire

Couleur du fond d’écran.

–

Comment changer la couleur du fond de l’écran ou de l’espace de travail ?

La fonction background ()

Définit la couleur utilisée pour l’arrière-plan de la fenêtre Processing. Le fond par défaut est gris clair. Cette fonction est généralement utilisée dans draw () pour effacer la fenêtre d’affichage au début de chaque image, mais elle peut également être utilisée dans setup () pour définir l’arrière-plan sur la première image de l’animation ou si l’arrière-plan n’a besoin d’être défini qu’une seule fois.

Une image peut également être utilisée comme arrière-plan pour une esquisse, bien que la largeur et la hauteur de l’image doivent correspondre à celles de la fenêtre d’esquisse. Les images utilisées avec background () ignorent le réglage de teinte actuel () . Pour redimensionner une image à la taille de la fenêtre d’esquisse, utilisez image.resize (largeur, hauteur).

Il n’est pas possible d’utiliser le paramètre alpha de transparence avec des couleurs d’arrière-plan sur la surface de dessin principale. Il ne peut être utilisé avec un PGraphics objet et CreateGraphics () .

//
//
// Comment changer la couleur du fond de l'ecran 
// ou de l'espace de travail dans processing
//
// H-Mazelin 12/06/2017


// La fonction setup () est exécutée une fois, lorsque le programme démarre. 
// Il sert à définir les propriétés d'environnement initiales telles que la 
// taille de l'écran et à charger des supports tels que des images et des polices
// au démarrage du programme. 


void setup ()
{
  // definition de la taile de la fenetre 
  // syntaxe : size (Hauteur fenetre,largeur fenetre )
  size(1000,400);
  // choix de la couleur du fond de la fenetre 
  // syntaxe : background (rouge,vert,bleu )
  // valeur du rouge de 0 à 255 iden pour les autre couleurs
  // affichage du fond de l'ecran en blanc 
  background(255,255,255);
  
}


//Le programme principal s’exécute par une boucle infinie appelée draw () 
void draw ()

{
  //Temporisation de 2000 soit 2 secondes
  delay(2000);
  // choix de la couleur du fond de la fenetre 
  // syntaxe : background (rouge,vert,bleu )
  // valeur du rouge de 0 à 255 iden pour les autre couleurs
  // affichage du fond en jaune 
  background(255,255,128);
  
  
}

// Comment changer la couleur du fond de l'ecran

// ou de l'espace de travail dans processing

// H-Mazelin 12/06/2017

// La fonction setup () est exécutée une fois, lorsque le programme démarre.

// Il sert à définir les propriétés d'environnement initiales telles que la

// taille de l'écran et à charger des supports tels que des images et des polices

// au démarrage du programme.

void setup ()

{

// definition de la taile de la fenetre

// syntaxe : size (Hauteur fenetre,largeur fenetre )

size(1000,400);

// choix de la couleur du fond de la fenetre

// syntaxe : background (rouge,vert,bleu )

// valeur du rouge de 0 à 255 iden pour les autre couleurs

// affichage du fond de l'ecran en blanc

background(255,255,255);

}

//Le programme principal s’exécute par une boucle infinie appelée draw ()

void draw ()

{

//Temporisation de 2000 soit 2 secondes

delay(2000);

// choix de la couleur du fond de la fenetre

// syntaxe : background (rouge,vert,bleu )

// valeur du rouge de 0 à 255 iden pour les autre couleurs

// affichage du fond en jaune

background(255,255,128);

}

Retour au sommaire

Différentes formes

Le rectangle (a,b,c,d)

Dessine un rectangle à l’écran. Un rectangle est une forme à quatre côtés avec chaque angle à quatre-vingt-dix degrés. Par défaut, les deux premiers paramètres définissent l’emplacement du coin supérieur gauche, le troisième définit la largeur et le quatrième définit la hauteur. La manière dont ces paramètres sont interprétés peut toutefois être modifiée avec la fonction rectMode () .

Pour dessiner un rectangle arrondi, ajoutez un cinquième paramètre, utilisé comme valeur de rayon pour les quatre coins.

Pour utiliser une valeur de rayon différente pour chaque coin, incluez huit paramètres. Lorsque vous utilisez huit paramètres, les quatre derniers définissent le rayon de l’arc à chaque coin séparément, en commençant par le coin supérieur gauche et en se déplaçant dans le sens des aiguilles d’une montre autour du rectangle.

Syntaxe :

rect ( a , b , c , d )
rect ( a , b , c , d , r )
rect ( a , b , c , d , t1 , tr , br , bl )

Paramétre :

a => coordonnée x du rectangle
b => coordonnée y du rectangle
c => largeur du rectangle
d => hauteur du rectangle
tl => rayon pour le coin supérieur gauche
tr => rayon pour le coin supérieur droit
br => rayon pour le coin inférieur droit
bl => rayon pour le coin inférieur gauche

Retour au sommaire

Tableau des différentes formes dans Processing
( utilisable avec la version Processing 3.3.4 ) .

Syntaxe	Description
point(`x`, `y`);	Dessine un point de grosseur de un pixel localisé dans la fenêtre en x et y x => coordonnée x du point y => coordonnée y du point – Exemple : Positionnement d’un point sur l’écran
point(`x`, `y`, `z`);	Dessine un point de grosseur de un pixel localisé dans la fenêtre en x et y .La 3^éme valeur étant optionnelle est la valeur de profondeur.Pour la création de ce point en 3D cela nécessite le paramètre P3D en combinaison avec la taille size() x => coordonnée x du point y => coordonnée y du point z => z-coordonnée du point
line(`x1`, `y1`, `x2`, `y2`);	Dessine une ligne à l’écran .Les lignes 2D sont dessinées avec une largeur d’un pixel par défaut . x1 => coordonnée x du premier point Y1 => coordonnée y ( vertical ) du premier point x2 => coordonnée x du deuxième point y2 => coordonnée y du deuxième point
line(`x1`, `y1`, `z1`, `x2`, `y2`, `z2`);	La version avec 6 paramètres permet de placer la ligne n’importe où dans l’espace XYZ. Pour la création de cette ligne en 3D cela nécessite le paramètre P3D en combinaison avec la taille size() x1 => coordonnée x du premier point y1 => coordonnée y ( vertical ) du premier point x2 => coordonnée x du deuxième point y2 => coordonnée y du deuxième point z1 => z-coordonnée du premier point z2 => z-coordonnée du deuxième point
rect(`a`, `b`, `c`, `d`);	Dessine un rectangle à l’écran avec tous les angles à 90° a => coordonnée x du rectangle b => coordonnée y du rectangle c => largeur du rectangle d => hauteur du rectangle
rect(`a`, `b`, `c`, `d`, `r`);	Dessine un rectangle arrondi à l’écran , ajoutez un 5 ^éme paramètre, qui est utilisé comme valeur de rayon pour les quatre coins. a => coordonnée x du rectangle b => coordonnée y du rectangle c => largeur du rectangle d => hauteur du rectangle r => rayons pour les 4 coins
rect(`a`, `b`, `c`, `d`, `tl`, `tr`, `br`, `bl`);	Dessiner un rectangle avec un rayon différent pour chaque coin . a => coordonnée x du rectangle b => coordonnée y du rectangle c => largeur du rectangle d => hauteur du rectangle tl => rayon pour le coin supérieur gauche tr => rayon pour le coin supérieur droit br => rayon pour le coin inférieur droit bl => rayon pour le coin inférieur gauche – Retour au sommaire
ellipse(`a`, `b`, `c`, `d`);	Dessine une ellipse (ovale) à l’écran. Une ellipse de même largeur et hauteur est un cercle. Les 2 premiers paramètres définissent l’emplacement sur l’écran . a => coordonnée x de l’ellipse b => coordonnée y de l’ellipse c => largeur de l’ellipse d => hauteur de l’ellipse – Retour au sommaire
triangle(`x1`, `y1`, `x2`, `y2`, `x3`, `y3`);	Le triangle est une forme constituée de trois points x1 => coordonnée x du premier point y1 => coordonnée y du premier point x2 => coordonnée x du 2 ^éme point y2 => coordonnée y du 2^éme point x3=> coordonnée x du 3 ^éme point y3 => coordonnée y du 3 ^éme point – Retour au sommaire
arc(x,y,l,h, start, stop );	x , y définissent le centre du cercle, l et h définissent la dimension du cercle l pour largeur, h pour la hauteur, start et stop sont les paramètres qui définissent le début et la fin de l’arc. x => coordonnée x de l’ellipse de l’arc y => coordonnée y de l’ellipse de l’arc l => largeur de l’ellipse de l’arc h => hauteur de l’ellipse de l’arc start => angle pour démarrer l’arc, spécifié en radians stop => angle pour arrêter l’arc, spécifié en radians Retour au sommaire
bezier (ax,ay,c1x,c1y,c2x,c2y,bx,by)	Pour dessiner une courbe de bézier, il faut définir quatre points avec chaque fois 2 valeurs (x,y) . La première et la dernière définiront le début et le fin de la courbe. Les deux points intermédiaires définiront les contrôles de courbe ax,ay => définition du début de la courbe c1x,c1y => premier contrôle de courbure c2x,c2y => deuxième contrôle de courbure bx,by => définition de la fin de la courbe – Exemple : La création d’un regard avec l’utilisation de la fonction courbe de Bezier et la fonction ellipse. Retour au sommaire

A savoir : La fonction delay ne peut être utilisé pour ralentir le dessin .

–

Le point :

Le point est l’équivalent d’un pixel localisé dans la fenêtre ou l’espace de travail

Syntaxe : point(x,y) ;

Exemple de programme sur le point :

Exemple de positionnement d’un point sur l’écran.
Exemple de création d’une ligne avec un ensemble de points

Exemple de positionnement d’un point sur l’écran :

//
//
//
// Positionnement d'un point sur l’écran 
//
// H-Mazelin 12/01/2017


// La fonction setup () est exécutée une fois, lorsque le programme démarre. 
// Il sert à définir les propriétés d'environnement initiales telles que la 
// taille de l'écran et à charger des supports tels que des images et des polices
// au démarrage du programme. 


void setup ()
{
  // definition de la taile de la fenetre 
  // syntaxe : size (Hauteur fenetre,largeur fenetre )
  size(800,600);
  // choix de la couleur du fond de la fenetre 
  // syntaxe : background (rouge,vert,bleu )
  // valeur du rouge de 0 à 255 iden pour les autre couleurs
  background(255,255,255); 
  
}


//Le programme principal s’exécute par une boucle infinie appelée draw () 

void draw ()

{
  
  // point(x,y) ; ->  x correspond à la largeur pour l'axe horizontal
  // et y à la hauteur pour l'axe vertical
  point (50,50);
  
  
}

// Positionnement d'un point sur l’écran

// H-Mazelin 12/01/2017

// La fonction setup () est exécutée une fois, lorsque le programme démarre.

// Il sert à définir les propriétés d'environnement initiales telles que la

// taille de l'écran et à charger des supports tels que des images et des polices

// au démarrage du programme.

void setup ()

{

// definition de la taile de la fenetre

// syntaxe : size (Hauteur fenetre,largeur fenetre )

size(800,600);

// choix de la couleur du fond de la fenetre

// syntaxe : background (rouge,vert,bleu )

// valeur du rouge de 0 à 255 iden pour les autre couleurs

background(255,255,255);

}

//Le programme principal s’exécute par une boucle infinie appelée draw ()

void draw ()

{

// point(x,y) ; -> x correspond à la largeur pour l'axe horizontal

// et y à la hauteur pour l'axe vertical

point (50,50);

}

Retour au sommaire

Exemple de création d’une ligne avec un ensemble de point

//
//
//
// création d'une ligne avec un ensemble de point  
//
// H-Mazelin 12/01/2017


// La fonction setup () est exécutée une fois, lorsque le programme démarre. 
// Il sert à définir les propriétés d'environnement initiales telles que la 
// taille de l'écran et à charger des supports tels que des images et des polices
// au démarrage du programme. 

// Déclaration de la variable x 
 int x;


void setup ()
{
  // definition de la taile de la fenetre 
  // syntaxe : size (Hauteur fenetre,largeur fenetre )
  size(800,600);
  // choix de la couleur du fond de la fenetre 
  // syntaxe : background (rouge,vert,bleu )
  // valeur du rouge de 0 à 255 iden pour les autre couleurs
  background(255,255,255); 
  
  
  
}


//Le programme principal s’exécute par une boucle infinie appelée draw () 

void draw ()

{
    
  
// Boucle comptant de 0 a 100 avec un increment de 1
// for (initialisation ; condition ; increment)
// entre crochet { instructions executees dans la boucle }
  
 
  for (x=0;x<100;x++)
   {
    
   // point(x,y) ; ->  x correspond à la largeur pour l'axe horizontal
   // et y à la hauteur pour l'axe vertical
   // a chaque passage dans la boucle on ajoute la valeur de x 
   point (50+x,50+x);
   
   }
 
  
  
}

// création d'une ligne avec un ensemble de point

// H-Mazelin 12/01/2017

// La fonction setup () est exécutée une fois, lorsque le programme démarre.

// Il sert à définir les propriétés d'environnement initiales telles que la

// taille de l'écran et à charger des supports tels que des images et des polices

// au démarrage du programme.

// Déclaration de la variable x

int x;

void setup ()

{

// definition de la taile de la fenetre

// syntaxe : size (Hauteur fenetre,largeur fenetre )

size(800,600);

// choix de la couleur du fond de la fenetre

// syntaxe : background (rouge,vert,bleu )

// valeur du rouge de 0 à 255 iden pour les autre couleurs

background(255,255,255);

}

//Le programme principal s’exécute par une boucle infinie appelée draw ()

void draw ()

{

// Boucle comptant de 0 a 100 avec un increment de 1

// for (initialisation ; condition ; increment)

// entre crochet { instructions executees dans la boucle }

for (x=0;x<100;x++)

{

// point(x,y) ; -> x correspond à la largeur pour l'axe horizontal

// et y à la hauteur pour l'axe vertical

// a chaque passage dans la boucle on ajoute la valeur de x

point (50+x,50+x);

}

Retour au sommaire

La courbe de Bézier :

Pour dessiner une courbe de bézier, il faut définir quatre points avec chaque fois 2 valeurs (x,y) . La première et la dernière définiront le début et le fin de la courbe. Les deux points intermédiaires définiront les contrôles de courbe

bezier (ax,ay,c1x,c1y,c2x,c2y,bx,by);

ax,ay => définition du début de la courbe
c1x,c1y => premier contrôle de courbure
c2x,c2y => deuxième contrôle de courbure
bx,by => définition de la fin de la courbe

–

Exemple d’utilisation de la courbe de Bézier :

La création d’un regard avec l’utilisation de la fonction courbe de Bezier et la fonction ellipse.

Tutoriel :

–

Programme du tuto ci-dessus

//
//
//
// création d'un regard avec  l'utilisation de la 
// courbe de Bezier et la fonction ellipse
//
// Version de IDE:Processing 3.3.4
// RedOhm
// H-Mazelin 12/07/2017

// Déclaration des variables
// Une variable est une donnée que l'ordinateur va stocker dans l'espace de sa mémoire
// Il existe différents type de variables:
// dans notre exemple .
// int =>Les nombres entiers peuvent être compris entre 2 147 483 647 à - 2 147 483 648
// float => pour les nombres à virgule flottante " qui posséde un point décimal " 

// Modification de la valeur du premier rayon de courbure de mes yeux
int be1;
// Modification de la valeur du deuxième rayon de courbure de mes yeux
int be2;
// Valeur de déplacement de mes yeux 
int deplace_x;
// Intervalle aléatoire pour le clignotement des yeux
float r;
// Intervalle aléatoire pour le déplacement des yeux
float deplacement_x;





// La fonction setup () est exécutée une fois, lorsque le programme démarre. 
// Il sert à définir les propriétés d'environnement initiales telles que la 
// taille de l'écran et à charger des supports tels que des images et des polices
// au démarrage du programme. 

void setup ()
{
  // definition de la taile de la fenetre 
  // syntaxe : size (Hauteur fenetre,largeur fenetre )
  size(1000,600);
  
  
  
}





//Le programme principal s’exécute par une boucle infinie appelée draw () 

void draw ()

{
  
 // ************* clignotement des paupieres ****************************

 // Fonction random(valeur_mini,valeur_maxi)
 // Cette fonction génère 1 nombre aléatoire. Chaque fois que cette fonction
 // est sollicitée dans le programme, le nombre aléatoire sera compris entre
 // la valeur mini et maxi fixée entre parenthèses  
 r = random(1,20);
 
 if (r>5 && r<6 )
 {
   // transfert des valeurs pour le clignotement des paupieres
   be1=180;
   be2=170;
 }
 else 
 {
   // transfert des valeurs par defaut
   be1=160;
   be2=140;
 }
 
 // ******** fin du teste de clignotement pour les paupieres ***********
 
 
 // ************* deplacement des yeux      ****************************

 // Fonction random(valeur_mini,valeur_maxi)
 // Cette fonction génère 1 nombre aléatoire. Chaque fois que cette fonction
 // est sollicitée dans le programme, le nombre aléatoire sera compris entre
 // la valeur mini et maxi fixée entre parenthèses 
 deplacement_x = random(1,40);
 
 
 
 // La ligne ci-dessous teste si le nombre aléatoire est compris entre la valeur
 // 5 et 6 si tel est le cas nous transférons la nouvelle valeur dans la variable
 // "déplacent_x", ce qui nous permettra de  faire bouger l’œil.
 
 if (deplacement_x>5 && 6<deplacement_x )
 {
   // force la variable à 8  
   deplace_x= 8;
   
 }
 else 
 {
   // force la variable à 0
   deplace_x= 0;
   
 }
 
 // ************* fin deplacement des yeux      ****************************
 
 

 
  
 // choix de la couleur du fond de la fenetre 
 // syntaxe : background (rouge,vert,bleu )
 // valeur du rouge de 0 à 255 iden pour les autre couleurs 
 background(0,0,0);  
  
 // Définit la couleur utilisée pour remplir les formes.
 // dans notre exemple 255 = noir
 fill(255);
 


 // **************** Oeil gauche *************************
 
 // bezier (ax,ay,c1x,c1y,c2x,c2y,bx,by);
 // ax,ay => definition du debut de la courbe
 // c1x,c1y => premier controle de courbure
 // c2x,c2y => deuxieme controle de courbure
 // bx,by => definition de la fin de la courbe 
 // bezier(10,100, 50,50, 150,50, 190,100); 
 bezier(300,176,350,be2,400,be1,450,200);
 bezier(300,176,350,230,400,220,450,200);

 
 // **************** Oeil droit *************************
 
 // bezier (ax,ay,c1x,c1y,c2x,c2y,bx,by);
 // ax,ay => definition du debut de la courbe
 // c1x,c1y => premier controle de courbure
 // c2x,c2y => deuxieme controle de courbure
 // bx,by => definition de la fin de la courbe 
 // bezier(10,100, 50,50, 150,50, 190,100);
 bezier(550,200,600,be1,650,be2,700,176);
 bezier(550,200,600,220,650,230,700,176);
 
 // Dessine une ellipse (ovale) à l’écran. Une ellipse de
 // même largeur et hauteur est un cercle. Les 2 premiers
 // paramètres définissent l’emplacement sur l’écran .
 // ellipse(a, b, c, d);
 // a => coordonnée x de l’ellipse
 // b => coordonnée y de l’ellipse
 // c => largeur de l’ellipse
 // d => hauteur de l’ellipse
 ellipse(380+deplace_x,193,35,35);
 ellipse(610+deplace_x,193,35,35);
 
 // Définit la couleur utilisée pour remplir les formes.
 // dans notre exemple le gris 
 fill(128,128,128);
 
 ellipse(380+deplace_x,193,10,10);
 ellipse(610+deplace_x,193,10,10);
 
 // La fonction println () écrit sur la zone de la console,
 // le rectangle noir au bas de l'environnement de traitement.
 // Cette fonction est souvent utile pour regarder les données
 // générées par un programme. 
 print("Valeur du nombre aleatoire pour le clignotement de yeux => "+ r);
 println("       Valeur du nombre aleatoire pour le deplacement des yeux => "+ r);
 
 // La fonction delay () arrête l'execution du programme  pendant un temps spécifié.
 // Les délais sont spécifiés en millièmes de seconde. Par exemple,
 // le délai d' exécution (3000) arrête le programme pendant trois
 // secondes et le délai (500) arrête le programme pendant une demi-seconde. 
 delay(100);
  
}

100

101

102

103

104

105

106

107

108

109

110

111

112

113

114

115

116

117

118

119

120

121

122

123

124

125

126

127

128

129

130

131

132

133

134

135

136

137

138

139

140

141

142

143

144

145

146

147

148

149

150

151

152

153

154

155

156

157

158

159

160

161

162

163

164

165

166

167

168

169

170

171

172

173

174

175

176

177

178

179

180

// création d'un regard avec l'utilisation de la

// courbe de Bezier et la fonction ellipse

// Version de IDE:Processing 3.3.4

// RedOhm

// H-Mazelin 12/07/2017

// Déclaration des variables

// Une variable est une donnée que l'ordinateur va stocker dans l'espace de sa mémoire

// Il existe différents type de variables:

// dans notre exemple .

// int =>Les nombres entiers peuvent être compris entre 2 147 483 647 à - 2 147 483 648

// float => pour les nombres à virgule flottante " qui posséde un point décimal "

// Modification de la valeur du premier rayon de courbure de mes yeux

int be1;

// Modification de la valeur du deuxième rayon de courbure de mes yeux

int be2;

// Valeur de déplacement de mes yeux

int deplace_x;

// Intervalle aléatoire pour le clignotement des yeux

float r;

// Intervalle aléatoire pour le déplacement des yeux

float deplacement_x;

// La fonction setup () est exécutée une fois, lorsque le programme démarre.

// Il sert à définir les propriétés d'environnement initiales telles que la

// taille de l'écran et à charger des supports tels que des images et des polices

// au démarrage du programme.

void setup ()

{

// definition de la taile de la fenetre

// syntaxe : size (Hauteur fenetre,largeur fenetre )

size(1000,600);

}

//Le programme principal s’exécute par une boucle infinie appelée draw ()

void draw ()

{

// ************* clignotement des paupieres ****************************

// Fonction random(valeur_mini,valeur_maxi)

// Cette fonction génère 1 nombre aléatoire. Chaque fois que cette fonction

// est sollicitée dans le programme, le nombre aléatoire sera compris entre

// la valeur mini et maxi fixée entre parenthèses

r = random(1,20);

if (r>5 && r<6 )

{

// transfert des valeurs pour le clignotement des paupieres

be1=180;

be2=170;

}

else

{

// transfert des valeurs par defaut

be1=160;

be2=140;

}

// ******** fin du teste de clignotement pour les paupieres ***********

// ************* deplacement des yeux ****************************

// Fonction random(valeur_mini,valeur_maxi)

// Cette fonction génère 1 nombre aléatoire. Chaque fois que cette fonction

// est sollicitée dans le programme, le nombre aléatoire sera compris entre

// la valeur mini et maxi fixée entre parenthèses

deplacement_x = random(1,40);

// La ligne ci-dessous teste si le nombre aléatoire est compris entre la valeur

// 5 et 6 si tel est le cas nous transférons la nouvelle valeur dans la variable

// "déplacent_x", ce qui nous permettra de faire bouger l’œil.

if (deplacement_x>5 && 6<deplacement_x )

{

// force la variable à 8

deplace_x= 8;

}

else

{

// force la variable à 0

deplace_x= 0;

}

// ************* fin deplacement des yeux ****************************

// choix de la couleur du fond de la fenetre

// syntaxe : background (rouge,vert,bleu )

// valeur du rouge de 0 à 255 iden pour les autre couleurs

background(0,0,0);

// Définit la couleur utilisée pour remplir les formes.

// dans notre exemple 255 = noir

fill(255);

// **************** Oeil gauche *************************

// bezier (ax,ay,c1x,c1y,c2x,c2y,bx,by);

// ax,ay => definition du debut de la courbe

// c1x,c1y => premier controle de courbure

// c2x,c2y => deuxieme controle de courbure

// bx,by => definition de la fin de la courbe

// bezier(10,100, 50,50, 150,50, 190,100);

bezier(300,176,350,be2,400,be1,450,200);

bezier(300,176,350,230,400,220,450,200);

// **************** Oeil droit *************************

// bezier (ax,ay,c1x,c1y,c2x,c2y,bx,by);

// ax,ay => definition du debut de la courbe

// c1x,c1y => premier controle de courbure

// c2x,c2y => deuxieme controle de courbure

// bx,by => definition de la fin de la courbe

// bezier(10,100, 50,50, 150,50, 190,100);

bezier(550,200,600,be1,650,be2,700,176);

bezier(550,200,600,220,650,230,700,176);

// Dessine une ellipse (ovale) à l’écran. Une ellipse de

// même largeur et hauteur est un cercle. Les 2 premiers

// paramètres définissent l’emplacement sur l’écran .

// ellipse(a, b, c, d);

// a => coordonnée x de l’ellipse

// b => coordonnée y de l’ellipse

// c => largeur de l’ellipse

// d => hauteur de l’ellipse

ellipse(380+deplace_x,193,35,35);

ellipse(610+deplace_x,193,35,35);

// Définit la couleur utilisée pour remplir les formes.

// dans notre exemple le gris

fill(128,128,128);

ellipse(380+deplace_x,193,10,10);

ellipse(610+deplace_x,193,10,10);

// La fonction println () écrit sur la zone de la console,

// le rectangle noir au bas de l'environnement de traitement.

// Cette fonction est souvent utile pour regarder les données

// générées par un programme.

print("Valeur du nombre aleatoire pour le clignotement de yeux => "+ r);

println(" Valeur du nombre aleatoire pour le deplacement des yeux => "+ r);

// La fonction delay () arrête l'execution du programme pendant un temps spécifié.

// Les délais sont spécifiés en millièmes de seconde. Par exemple,

// le délai d' exécution (3000) arrête le programme pendant trois

// secondes et le délai (500) arrête le programme pendant une demi-seconde.

delay(100);

}

Retour au sommaire

Utilisation de la souris dans Processing

–

Variable système attachées à l’utilisation de la souris

Syntaxe	Description
mouseX	La variable système mouseX contient toujours la coordonnée horizontale actuelle de la souris.
mouseY	La variable système mouseY contient toujours la coordonnée verticale actuelle de la souris.
pmouseX	La variable système pmouseX contient toujours la position horizontale de la souris dans le cadre antérieur à la trame actuelle.
pmouseY	La variable système pmouseY contient toujours la position verticale de la souris dans le cadre antérieur à la trame actuelle.
mousePressed	La variable mousePressed stocke si un bouton de la souris est ou non pressé. La valeur est vraie lorsque l’on appuie sur un bouton de la souris et à contrario est faux si aucun bouton n’est appuyé.
mouseReleased ()	La fonction mouseReleased () est appelée chaque fois qu’un bouton de souris est relâché.
mouseClicked ()	La fonction mouseClicked () est appelée après avoir appuyé sur un bouton de la souris puis relâché.
mouseMoved ()	La fonction mouseMoved () est appelée chaque fois que la souris se déplace et que le bouton de la souris n’est pas appuyé. (Si un bouton est pressé, mouseDragged () est appelé à la place.)
mouseDragged ()	La fonction mouseDragged () est appelée à chaque fois que la souris se déplace et si vous appuyez sur un bouton de la souris. (Si un bouton n’est pas pressé, mouseMoved () est appelé à la place.)
mouseButton	Quand un bouton de la souris est enfoncé, la valeur de la variable système mouseButton est réglé sur GAUCHE , DROITE , ou CENTRE , selon le bouton qui est enfoncé. (Si aucun bouton n’est appuyé, le bouton de la souris peut être réinitialisé à 0. Pour cette raison, il est préférable d’ utiliser en premier MousePressed pour tester si un bouton est pressé et seulement ensuite tester la valeur de mouseButton
mouseWheel()	La fonction mouseWheel () renvoie des valeurs positives lorsque la roue de la souris est basculée vers le bas (vers l’utilisateur) et des valeurs négatives pour l’autre sens

Retour au sommaire

Un cercle qui suit les mouvements de votre souris

//
//
// Un cercle qui suit les mouvements de votre souris 
//
//
// H-Mazelin






// Declaration de x dans une variable du type int ( nombre entier )
int x;
// Declaration de y dans une variable du type int ( nombre entier )
int y;



// La fonction setup () est exécutée une fois, lorsque le programme démarre. 
// Il sert à définir les propriétés d'environnement initiales telles que la 
// taille de l'écran et à charger des supports tels que des images et des polices
// au démarrage du programme. 
void setup ()
{
  // definition de la taile de la fenetre 
  // syntaxe : size (Hauteur fenetre,largeur fenetre )
  size(1000,400);
  // choix de la couleur du fond de la fenetre 
  // syntaxe : background (rouge,vert,bleu )
  // valeur du rouge de 0 à 255 iden pour les autre couleurs
  // affichage du fond de l'ecran en blanc 
  background(255,255,255);
  
}





//Le programme principal s’exécute par une boucle infinie appelée draw ()

void draw()

{
  
  // Definition de la position sur l'espace de travail avec x et y
  // les valeurs x et y correspond au coin superieur gauche de l'espace 
  // de travail 
  // x = position du centre en horizontal
  // y = position du centre en vertical
  // a = diametre sur l'axe horizontal
  // b = diametre sur l'axe vertical  
  // ellipse(x,y,a,b);
  ellipse(x, y, 30, 30);
  //la variable systeme mouseX contient la coordonnée horizontale 
  //de la souris 
  x=mouseX;
  //la variable systeme mouseY contient la coordonnée vertical 
  //de la souris 
  y=mouseY;
  
  
}

// Un cercle qui suit les mouvements de votre souris

// H-Mazelin

// Declaration de x dans une variable du type int ( nombre entier )

int x;

// Declaration de y dans une variable du type int ( nombre entier )

int y;

// La fonction setup () est exécutée une fois, lorsque le programme démarre.

// Il sert à définir les propriétés d'environnement initiales telles que la

// taille de l'écran et à charger des supports tels que des images et des polices

// au démarrage du programme.

void setup ()

{

// definition de la taile de la fenetre

// syntaxe : size (Hauteur fenetre,largeur fenetre )

size(1000,400);

// choix de la couleur du fond de la fenetre

// syntaxe : background (rouge,vert,bleu )

// valeur du rouge de 0 à 255 iden pour les autre couleurs

// affichage du fond de l'ecran en blanc

background(255,255,255);

}

//Le programme principal s’exécute par une boucle infinie appelée draw ()

void draw()

{

// Definition de la position sur l'espace de travail avec x et y

// les valeurs x et y correspond au coin superieur gauche de l'espace

// de travail

// x = position du centre en horizontal

// y = position du centre en vertical

// a = diametre sur l'axe horizontal

// b = diametre sur l'axe vertical

// ellipse(x,y,a,b);

ellipse(x, y, 30, 30);

//la variable systeme mouseX contient la coordonnée horizontale

//de la souris

x=mouseX;

//la variable systeme mouseY contient la coordonnée vertical

//de la souris

y=mouseY;

}

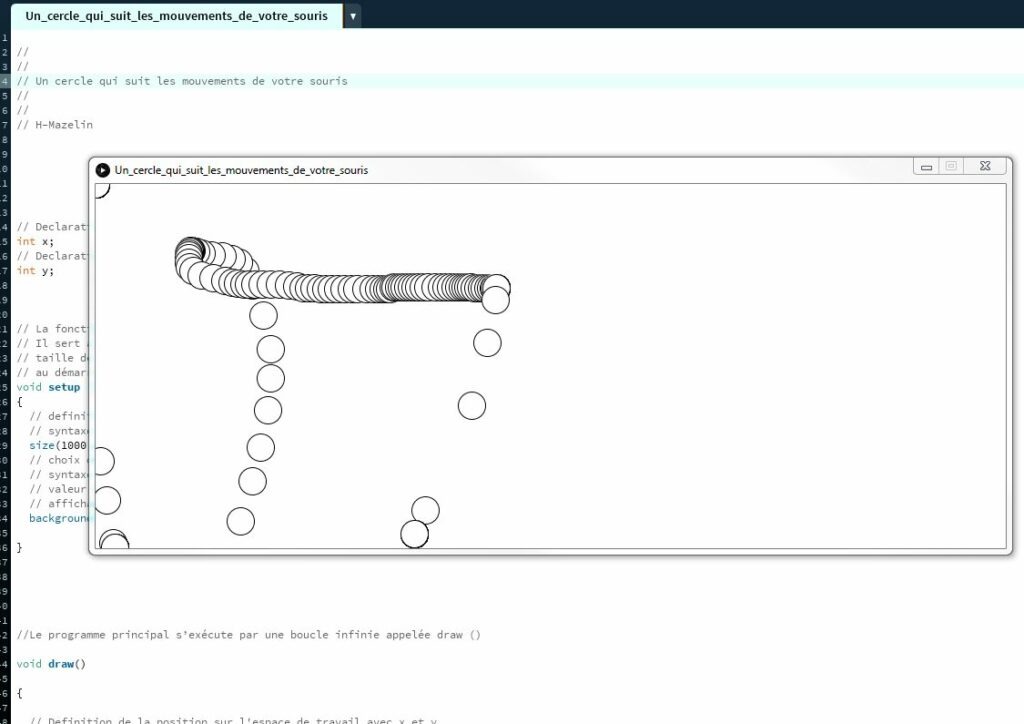
Processing : Un cercle qui suit les mouvement de votre souris – RedOhm

Retour au sommaire